Module 6

Repetition of Statements

As we have seen when looking at Algorithms such as Heron's (a.k.a. Hero's, a.k.a Babylonian Algorithm) to calculate a square root, in programming we have ample reasons to repeat the same (or slightly altered) group of statements (known as a "block"). Python implements two constructs: the more specialized for-loop and the more general while-loop, which we are going to meet soon.

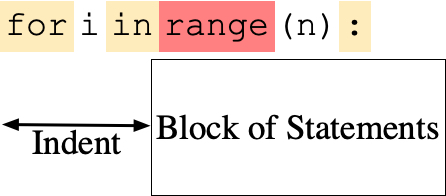
The for-loop in Python has an iteration variable. An example is given in the picture above. The first line for i in range(n): consists of the key-word "for", followed by the iteration variable, which in this case is called "i". This is followed by the "in" keyword, which then is followed by something that needs to generate iteratively values for i. The range(n) in this example will generate all of the integer values starting with 0 and terminating with n-1. For each of these values, the statements in the block are executed.

Python is different from the for-loop in C, C++, or Java, in that for loops are more general. For example, if we want to print out the letters of some user input on separate lines, we can use:

Here, the for loop causes all the letters of the input to become successively stored in the variable letter, which in the body of the for-loop, the indented statement, are then printed out.

The range keyword

The range keyword generates a sequence of numbers. The range construct is quite flexible. If there is a single parameter such as in range(7), then the range generates the numbers starting with 0 (this is a peculiarity in all of Computer Science that we start counting with 0) and finishing with 6, i.e. it generates 0, 1, 2, 3, 4, 5, 6. We stop with 6 because we generated 7 numbers. Thus, the parameter is called the stop value. If there are two parameters to range as in range(5,9) , then we generate 5, 6, 7, 8. Thus, the first parameter is the start value and the second parameter becomes the stop value. Finally, we can also specify a stride, that would be the third argument to range. For example, range(5, 14, 3) , the first value is still the start value, namely 5. But the second value is 5+3 = 8, since the stride is 3. We stop before the sequence reaches 14 or a higher number. Thus range(5, 14, 3) generates 5, 8, 11 and then stops because the next value would be 14. The stride can be negative, in which case the sequence goes backward. We still start with the start value, but stop just before the sequence reaches the stop value or below. Thus range(25, 14, -3) generates 25, 22, 19, and 16.

Calculating sums and products

A frequent pattern in this class is the calculation of sums of products. For example, let's calculate the following sum:

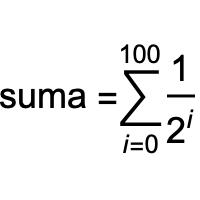
We notice that the index goes from 0 to 100, therefore the start value is 0 and the stop value is 101, not 100, because we want to include 100. We need to also have a variable to accomodate the partial sum; this is called an accumulator. This results in the code below, where I also print out the partial values of the accumulator.

Notice the use of the iteration variable i, how its range is being defined, and that the accumulator accu is initialized to zero and augmented throughout the loop. If you run the code, you will see that the accumulator quickly becomes 2.0, which is not quite the exact value, it should be 1/2**100 less, but floating point arithmetic is never exact. If the taks is to calculate a product, then the accumulator needs to be initialized to 1. If it were initialized to zero, then it would stay zero, whatever we multiply with it.